Definición:
Las ménsulas son vigas pequeñas en voladizo que se proyectan de la cara interior de las columnas para soportar cargas concentradas pesadas o reacciones de vigas.
El dimensionamiento correcto de las ménsulas es de gran importancia, ya que en ellas se apoya generalmente miembros estructurales de grandes dimensiones o equipo pesado.
Se diseñan en especial para suministrar la reacción vertical Vu en el extremo de la viga soportada, pero a menos que se tomen precauciones especiales para evitar las fuerzas horizontales que genera la retracción de fraguado restringida, el flujo plástico (en caso de vigas preesforzadas) o los cambios de temperatura, también
deben resistir una fuerza horizontal.
La relación del brazo o claro de cortante al peralte de la ménsula es con frecuencia menor de 1.00, (bw/d < 1).
Tipos de fallas:

Hipótesis de cortante por fricción para la transferencia de cortante en ménsulas:
Las ménsulas que no se cuelan al mismo tiempo que las columnas principales de apoyo pueden tener una grieta potencial de cortante en la superficie de contacto entre los dos concretos, a través de la cual se desarrolla la transferencia de cortante.
Cuanto más pequeña sea la relación a/d, mayor será la tendencia de que el cortante puro ocurra a través de planos esencialmente verticales.

El ACI recomienda en este caso la aproximación de cortante por fricción, como se muestra en la figura b; en la cual se supone un plano vertical ya agrietado a-a, a lo largo de la cual se considera que la ménsula se desliza conforme alcanza su estado límite de falla.
La fuerza cortante resistente nominal vertical es:
Vn = Avf * Fy *u
Avf = Vn / (∅ * Fy * u)
Donde:
u = coeficiente de fricción
Avf = Área total de estribos cerrados horizontales
El cortante vertical externo factorizado deberá ser:
Vu ≤ ∅ * Vn
Para concreto normal se escoge el menor de:
Vn ≤ 0.2 * F´c * bw * d
Vn ≤ 800 * bw * d
Coeficientes de fricción (ACI 318 – 02):
1.- Concreto colado monolíticamente = 1.4 λ
2.- Concreto colado sobre un concreto fraguado áspero = 1.0 λ
3.- Concreto colado sobre un concreto fraguado liso = 0.6 λ
4.- Concreto anclado a un acero estructural = 0.7 λ
Donde:
1.- λ = 1 para concreto de peso normal
2.- λ = 0.85 para concreto de arena de peso ligero
3.- λ = 0.75 para todo concreto ligero
Partes de las ménsulas:
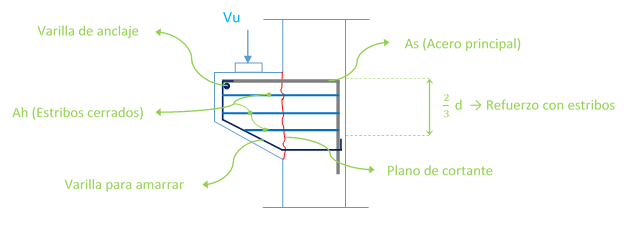
Efecto de la fuerza externa horizontal:
La fuerza externa factorizada “Nuc” no deberá exceder el cortante vertical factorizado “Vu”, por lo tanto se debe proporcionar acero de refuerzo “An” para resistir la fuerza “Nuc”.
An = Nuc/(∅*Fy)
y Af para resisitir los momentos flexionantes Vu y Nuc.
Af = (Vu*a+Nuc (h-d))/(∅*Fy*jd)
jd = 0.85 d
Nuc ≥ 0.2 Vu
También:
Af = Mu/(∅*Fy*jd)
Remplazando tenemos:
Af = Mu/(0.85*∅*Fy*d)
El área As del refuerzo principal de tensión se calcula con:
Se escoge el mayor de:
As ≥ 2/3*Avf+An
As ≥ Af+An
Para la cuantía se toma el mayor As:
⍴=As/bd ≥ 0.04 * (F´c)/Fy
Si se supone Ah como el área total de los estribos cerrados o estribos paralelos a As.
Ah ≥ 0.5 (As-An)
Secuencia de diseño de ménsulas:
En una ménsula actúan básicamente na fuerza horizontal factorizada “Nuc”, una fuerza vertical factorizada “Vu” y un momento flexionante [Vu*a+Nuc (h-d)].
Las ménsulas se deben diseñar para resistir estos tres parámetros simultáneamente, por medio de uno de los siguientes métodos:
a) Para ménsulas coladas monolíticamente con la columna de apoyo: determinar el área de acero Ah de los estribos cerrados los cuales se colocan debajo de los estribos principales As.
b) Calcular el área de hacer Avf si la ménsula y la columna no están coladas simultáneamente, utilizando parte de Avf a lo largo del peralte de la ménsula y agregando el restante en el área As del refuerzo principal superior.
c) Se calcula la fuerza vertical factorizada Vu y la fuerza resistente nominal Vn de la sección de manera que:
Vn ≥Vu/∅ ; ∅ = 0.85
Vu/∅ =0.2*F´c*bw*d ó ≤ 800*bw*d
Si no se cumple debe ser aumentada la sección del concreto en el apoyo
d) Para resistir la fuerza de cortante por fricción se calcula Avf:
Avf=Vn/(Fy*u)
e) Para calcular el acero principal de tensión superior As se aplica:
Acero por flexión Af:
Af=(Vu*a+Nuc (h-d))/(∅*Fy*jd)
An=Nuc/(∅*Fy)
f) Calculo del área del acero principal
Se escoge el mayor de:
As ≥ 2/3*Avf+An (1)
As ≥ Af+An (2)
Si rige el caso 1: el restante 1/3 Avf se deberá proporcionar como estribos cerrados paralelos a As y distribuidos en una distancia de 2/3 d, junto a A. Si rige el caso 2: utilice además 1/2 Af como estribos cerrados distribuido dentro de una distancia de 2/3 d, junto a As.
Ah≥0.5 (As-An)
⍴=As/bd ≥0.04
(F´c)/Fy o bien As min = 0.04 (F´c)/Fy b*d
g) Seleccione el tamaño y la separación del refuerzo de la ménsula con atención especial al detalle de la distribución, ya que muchas fallas de ménsulas se deben a detalles incorrectos.
Ejemplo:
Diseñar una ménsula para soportar una carga vertical factorizada Vu, actuando a una distancia a del paño de la columna. La ménsula tiene un ancho bw, un espesor total h y un peralte efectivo d. Suponga que la ménsula será; ya sea colada después de que la columna de apoyo sea construida, o ambas coladas simultáneamente.
Ejercicio resuelto en hoja de Excel adjuntada en el archivo de descarga.
Descarga el archivo completo en formato Excel y PDF a continuación.
DESCARGA SEGURA
ARTÍCULOS RELACIONADOS
– 1. Fuerza Cortante y Momento Flexionante en Vigas [Clic Aquí]
Para más información sobre: Libros, Normas, Archivos, Programas, Hojas de Cálculo, y todo lo relacionado con la Ingeniería Civil y el mundo de la Construcción; únete a nuestro grupo de Facebook con tan solo dar clic al siguiente enlace.
“Todo lo relacionado con la Ingeniería Civil y el mundo de la Construcción.”




1 comentario en «Ménsulas (Ejercicio Resuelto)»